Defining Clutch - Hype Moments in the NHL

Creating a Win Probability Model for hockey to classify shots as clutch.

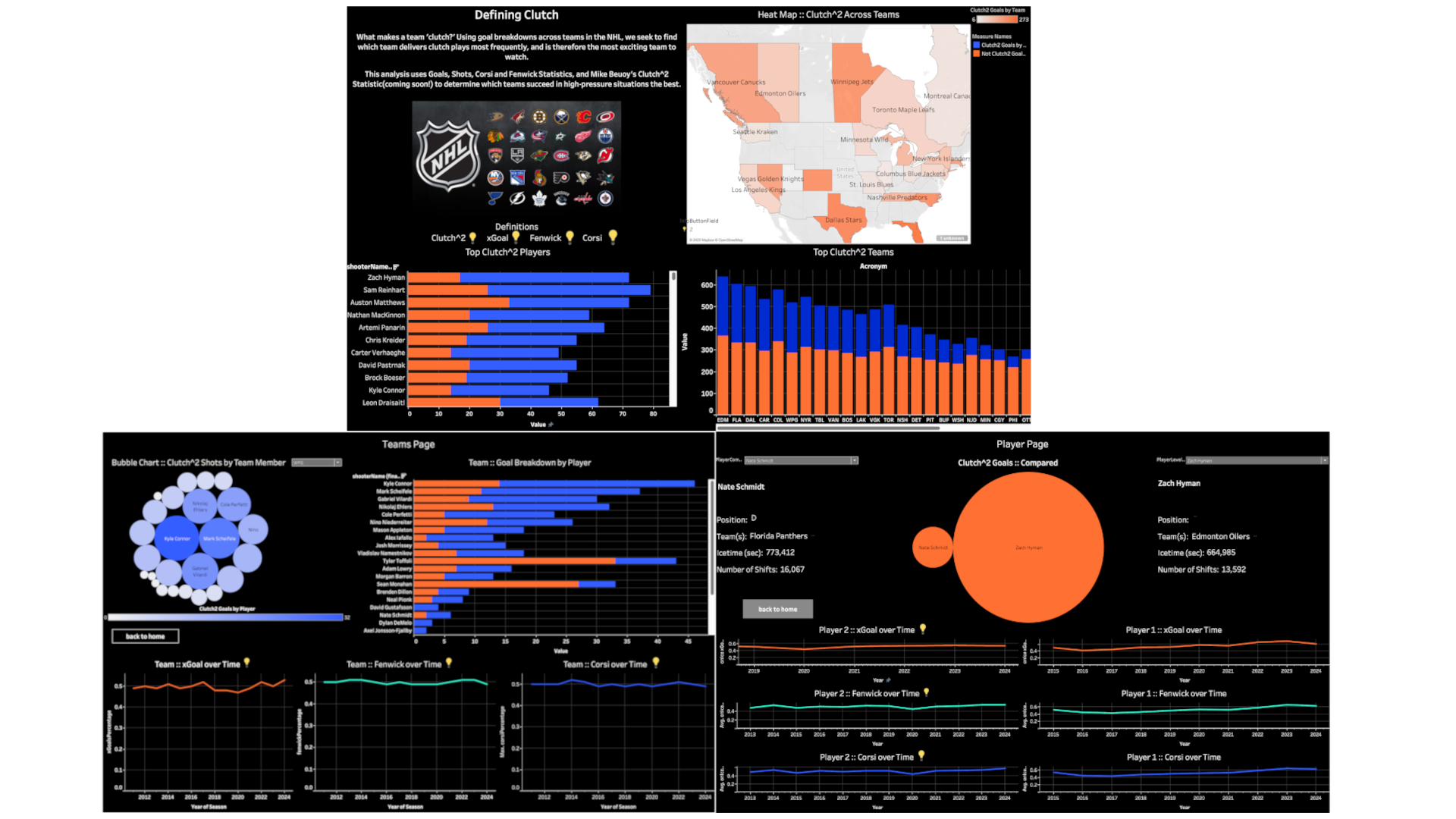
This project was the final project for my DS 4210 - Business Intelligence class at Tennessee Tech. The goal of this project was to create a Tableau Dashboard for NHL Players and Teams to illustrate mathematically which teams and players have the most "Clutch" moments, and are therefore the most exciting to watch. This was done by creating a simple Win Probability Model based on Stephen Pettigrew's Added Goal Value model, and using that to compute Mike Beuoy's Clutch² metric, which is our measure of "clutchness". This project was made by myself, Abhishek Menothu, and Jonathen Wigfall using Python, R, Excel, and Tableau.

What is Clutch?

The "Clutch Factor" is a term in sports that we hear a lot, but its definition is illusory. It can be written off as luck or a gene that only a handful of players possess, but what if clutch shooting could be defined mathematically? This is where Michael MacKelvie enters. His video The Clutch GOAT outlines clutch play in the NBA, and inspired our team to recreate this model in the NHL. MacKelvie's video uses Mike Beuoy's Clutch² model, which measures swings in Win Probability to identify key moments in a game that create a win.

Also in MacKelvie's video, he provides an NBA definition of clutch that we could apply to NHL plays. The definition of clutch in the NBA is "The final five minutes of the fourth quarter or overtime when the score is within five points". For hockey, we can trim the score differential down to within one goal, as those are the game-tying and game-winning moments in hockey. However, this still ranks a buzzer beater goal that sends a team to OT or secures a win the same as a goal scored with 4:59 left in the period that does not have the same intense, jump-out-of-your-seat impact that the former produces. For this reason, we decided to use Beuoy's Clutch² model as well to try to have a more robust clutch measure.

What is a Win Probability Model?

To classify shots as Clutch² or not, a win probability model needs to be constructed. Win Probability (WP or WPA for Win Probability Added) models are a model used to determine a team's probability of winning at any moment in the game given play-by-play (PBP) data. Unfortunately, the team was unable to get working play-by-play data for this project, and resorted to using the MoneyPuck shot dataset instead as a subset of total PBP data.

For the Win Probability Model, we used the Stephen Pettigrew Added Goal Value (AGV) model with the Basic Competing Poisson estimation from this paper by Alan Ryder. Pettigrew outlines the following model:

Where...

• $t$ is time remaining in the game.
• $P_t(w)$ is the probability of a win at time remaining, $t$.
• $\delta_t$ is the score differential(homeGoals minus awayGoals) at time remaining, $t$.
• $\gamma_h$ is a vector of goal-scoring rates (accessed from MoneyPuck Teams Data) at different non-even strengths ([5on4, 5on3, 4on3, 3on4, 3on5, 4on5] or [5on5, other, 4on5] from the Teams dataset).
• $\gamma_a$ is the same as $\gamma_h$, only in reverse order to correspond to the away team's scoring rate ([4on5, other, 5on4]).
• $\mathbf{\nu_t}$ is a vector of seconds remaining in each of the six non-even strength situations at time $t$, using penalty times for home in 4on5, 3on5 and 3on4, and away penalty times in 5on4, 5on3 and 4on3. Unfortunately, the Moneypuck data does not provide a way to use multiple times remaining across multiple penalties, so we are assuming that we just want to use the penalty time remaining at the index of current strength for each team, and use the penalty time corresponding to when the strength of either team changes, by any amount.
• $\Lambda$ is the Poisson PMF, evaluated at $P(x=1)^2$, and will be deployed using the scipy.stats package.

Additionally, the term $P_t(w \space | \space \delta_t)$ is the probability that the home team will win, given a score differential $\delta_t$. This is estimated with the following model from the Ryder paper.

Using these models with the combined shots from Moneypuck, we were able to create Win Probabilities of each game, then apply the following method to each game's win probability to classify shots as Clutch² or not. The shots with their classifications were then imported to Tableau and the dashboard was created.

Findings

With our model, we were able to rank players from the 2023-2024 and 2024 season by their "clutch-ness". We found that the top 5 teams by Clutch² goal count were: the Edmonton Oilers, Florida Panthers, Dallas Stars, Carolina Hurricanes, and the Colorado Avalanche.

The top 5 players by Clutch² goal count were: Zach Hyman(EDM), Sam Reinhart(FLA), Auston Matthews(TOR), Nathan MacKinnon(COL), and Artemi Panarin(NYR). These line up with the players who were most impactful in the 2023 season: Zach Hyman's incredible run in the playoffs, Auston Matthews with his 69-goal season, Sam Reinhart with his Stanley Cup-Winning performance, and MacKinnon and Panarin with their deep playoff runs. It was interesting to not see a players on the Stars or the Hurricanes showing up in the top 5, but this could be a a more even distribution of goals across players, versus a player like Hyman who scored a significant portion of the Oiler's goals.

Next Steps

There are some issues with the model that we hope to correct in the future. First, the data is an incomplete subset; we need to use a full play-by-play dataset. When we were trying to create our data, the NHL had just redone their entire API, hopefully for future iterations of the project that will be documented better.

Additionally, our WP model could be improved. This could be done using the standard XGBoost Model, or continuing with the Pettigrew model, with more Ryder estimations like PythagenPuck or PythagenPort. Ideally, we can get several models working, and then compare their results to get the best model possible for the dataset.

Lastly, some tweaks need to be made to this model and the data. We do not have a clutch observation in the model to compare the classifications against, this would need to be added to get the accuracy of our model. Additionally, the model currently does not start at a 50/50 (or weighted) probability of each team winning, so an initial probability of a win needs to be added. Lastly, the model does not handle overtime NHL goals. This is a crucial feature to add, as the "clutch-est" moments in hockey are the overtime goals that end a game or playoff series.

I am leaving a list here for myself to look at when I revisit the project.

• Get Play-By-Play Data
• Build XGBoost Model
• Classify Clutch Shots (use Game-Winning Goals, GWG), compare to Clutch² Shots
• Build Model with other Ryder estimations
• Compare Models
• Run on a larger dataset

Please reach out if you have comments or criticisms, I am still working on the comment section for this site.

All code can be found at my git repository, hockey-clutch2-model. If you would like to see the Tableau Dashboard, I can send a packaged version via email.

Resources

• Michael MacKelvie's Clutch GOAT video
• Mike Beuoy's Clutch/² Model
• Alan Ryder's Win Probabilities Paper
• Stephen Pettigrew's Added Goal Value Model Presentation
• Stephen Pettigrew's Added Goal Value Model Paper
• Peter Tanner's MoneyPuck